Портал | Содержание | О нас | Авторам | Новости | Первая десятка | Дискуссионный клуб | Чат Научный форум Первая десятка "Русского переплета" Темы дня:

Мир собирается объявить бесполётную зону в нашей Vselennoy! | Президенту Путину о создании Института Истории Русского Народа. |Нас посетило 40 млн. человек | Чем занимались русские 4000 лет назад? | Кому давать гранты или сколько в России молодых ученых?

Компоненты двойной системы пробными телами не назовешь. Движение одной из них определяется положением другой, и наоборот. Обе они вращаются вокруг друг друга. Но мы знаем, что центр масс замкнутой системы должен покоиться или равномерно двигаться. Влияние других звезд невелико. Обе звезды движутся точно так же, как планеты Солнечной системы, т. е. по эллипсам, в одном из фокусов которых расположен центр масс двойной системы (см. рис. 7).

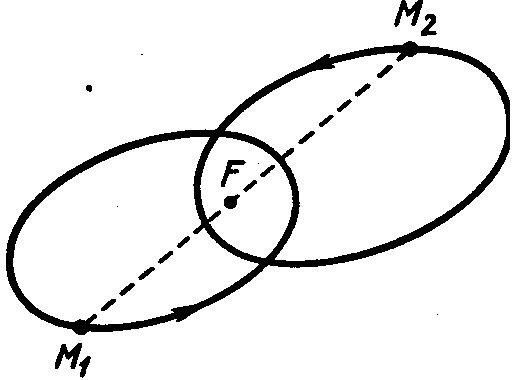
Рис. 8. Абсолютные орбиты звезд двойной системы.

Эти эллипсы называют абсолютными орбитами звезд. Столь высокое название просто подчеркивает, что эти орбиты построены в системе центра масс двойной.

Эллиптичность орбит двойных звезд доказывается прямыми наблюдениями ближайших двойных звезд (см. рис. 8). Правда, астрономам удобнее в этом случае измерять не абсолютную, а относительную орбиту.

1б

Обычно поступают следующим образом. Выбирают одну из звезд, считая ее неподвижной, и относительно нее измеряют положение второй звезды. Видимая орбита есть проекция истинной относительной орбиты на небесную сферу. Она тоже эллипс. (Немного подумав, читатель поймет, что если проекция окружности - эллипс, то

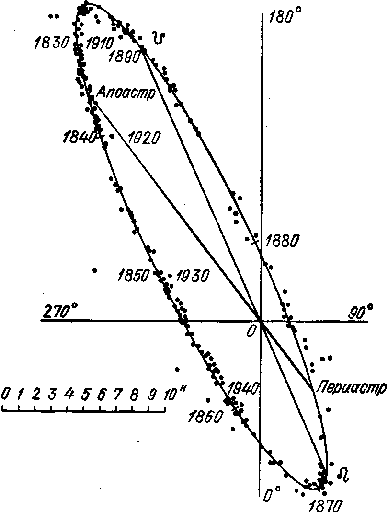
Рис. 8. Видимая орбита одной из звезд в двойной системе звезды альфа Центавра. Это ближайшая к нам из двойных, поэтому форма орбиты звезды вырисовывается по прямым наблюдениям. Яркая звезда на- ходится в точке О, положения спутника яркой звезды показаны точками. (Наблюдения проводились с 1830 по 1940 гг. Шкала показывает масштаб в угловых секундах.)

и проекция эллипса тоже эллипс.) Однако фокусы видимого и настоящего эллипсов не совпадают. Поэтому неподвижная звезда на рис. 8 находится не на оси видимой орбиты.

При движении звезды по эллипсу остается справедливым и второй закон Кеплера. А вот третий закон слегка изменяется. Это ясно. В формулу, связывающую период и размер орбиты, массы звезд должны входить равноправно:

a³/ P² = G (M₁ + M₂)/4 pi²

Если М₂ много меньше M₁ то M₂ можно просто выбросить из формулы, и мы получим третий закон Кеплера для планет.

Точка орбиты, в которой звезды сходятся на ближайшее расстояние, называется периастром, а точка максимального удаления - апоастром *). Очевидно, большая ось проходит через эти две точки. Ее иногда называют линией апсид **).

Кто главнее?