Законы Кеплера
Известный немецкий астроном Иоганн Кеплер после
окончания Тюбингенской академии распреде-
лился профессором математики и " нравственной философии " в одну из
гимназий. Так в 1593 г., т. е. за 17 лет до
изобретения телескопа, началась его научная карьера.
Впоследствии этот человек проявил себя не только великим теоретиком, но и не
менее выдающимся эксперимен-
татором. За 6 лет до того, как Галилео Галилей направил свой телескоп на
небо, Кеплер написал книгу
о приложении оптики к астрономии (!). Наиболее распространенные сейчас
системы школьных телескопов, в которых и объектив, и окуляр -
увеличительные линзы, изобретены Кеплером в 1611 г.
Но самые поразительные открытия Кеплер сделал,
что называется, " на кончике пера " . Кеплер не был теоретиком в
современном смысле слова. На современном
языке ближе к нему подходит определение " интерпретатор " . Говорят,
что интерпретатор - это человек, который
не наблюдает, но и не строит теорий - он приводит в порядок факты, ищет
закономерности. Правда, это не очень
точно. Кеплер свято верил в великую гармонию природы. Иногда эта вера
заводила его слишком далеко, но
в то же время он всегда опирался на четкие экспериментальные данные. А в
этом смысле ему особенно повезло.
В 1601 г. Кеплер оказался " наследником "
бесценного
состояния. В его руки попал архив наблюдений (дневник
наблюдений) великого астронома Тихо Браге. Девять лет
потратил Кеплер на анализ наблюдений планеты Марс.
В те времена ученые не писали научных статей. Не было
и периодически издаваемых научных журналов. Поэтому
свои исследования ученые излагали в книгах. Кеплер тоже написал книгу,
название которой стоит привести целиком: " Новая астрономия, причинно
обусловленная, или
физика неба, изложенная в исследованиях о движении
звезды Марс, по наблюдениям благороднейшего мужа
Тихо Браге ".
Здесь впервые Кеплер доложил, что Марс движется
по эллипсу, в одном из фокусов которого находится Солнце. Напомним, что
эллипс - это плоская кривая, представляющая собой геометрическое место
точек, сумма
расстояний которых от двух других его фиксированных
точек постоянна. (Эллипс легко нарисовать. Возьмите две
иголки и наколите их на лист бумаги. Места проколов -
это фокусы. Привязав к иголкам нитку, натяните ее
карандашом. Плавно передвигая карандаш, получите эллипс.
Ведь длина нитки постоянна.)
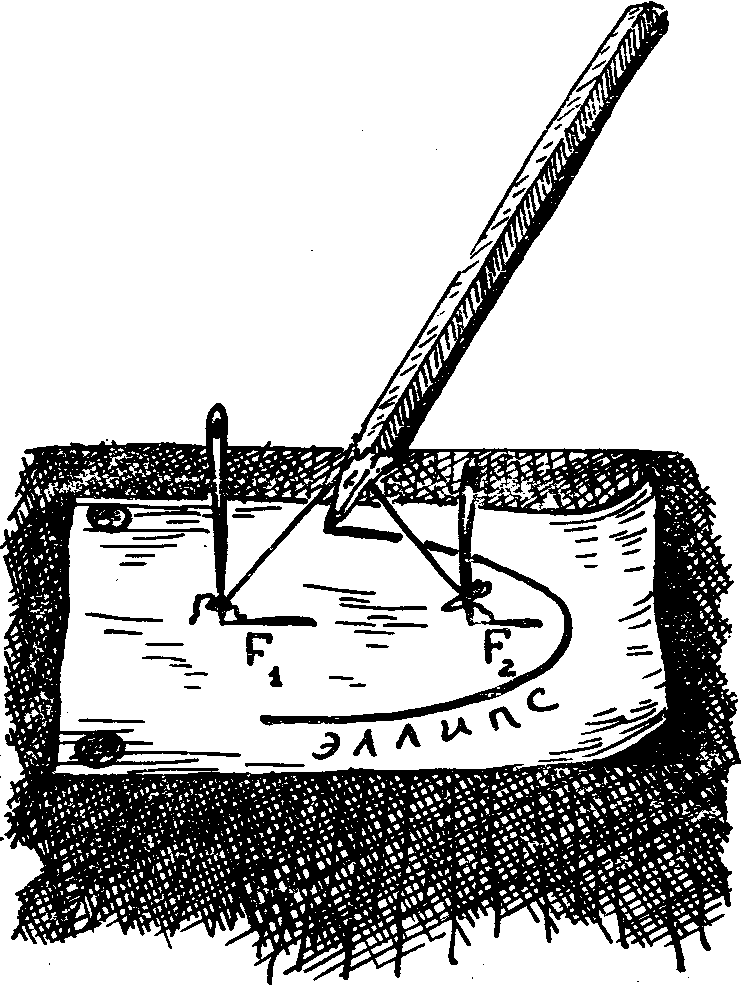
Как нарисовать эллипс
Одновременно Кеплер подметил, что движение Марса
неравномерное - при приближении к Солнцу он ускоряется, а при удалении -
замедляется. Но Кеплер везде
искал красоту. Оказалось, что площади, описываемые радиусом-вектором
планеты за
одинаковое время, одинаковы
(рис. 2).

Рис. 2. За равные промежутки времени ((д - ti
=
= (4 - (э) радиус-вектор
планеты описывает равновеликие площади (закон
Кеплера)
Через 10 лет Кеплер написал
еще одну книгу - " Гармония мира " , в которой сообщил, что точ-
но так же, как и Марс, движутся
и другие планеты. То есть все
планеты движутся по эллипсам,
в одном из фокусов которых находится Солнце (первый закон Кеплера), и всегда
за одинаковые
промежутки времени радиус-вектор планеты описывает равновеликие площади
(второй
закон Кеплера). Читатель может спросить: причем
тут красота, гармония? Ну, эллипс, ну, овал - какая
разница. А вы нарисуйте эллипс. Он гораздо красивее
овала. Вы скажете, что на вкус и цвет товарищей нет.
И все же эллипс - уникальная фигура. Потому что эллипс - это тень
круга, самой симметричной плоской фигуры.
Проекция круга - это не овал, а эллипс. Может
быть, поэтому эллипс кажется красивее.
Но есть в законах Кеплера и другая красота, имеющая
глубокий физический смысл. Ведь удивительно, по-
чему столь удаленные друг от друга и, казалось бы, совершенно независимые
планеты " знают " , что им нужно
двигаться по эллипсам. Когда мы рисуем эллипс на листке бумаги, все ясно.
Есть ниточка, которая держит карандаш. Меняя длину нитки, можно нарисовать
много фи-
гур, но все они будут эллипсами. Значит, во Вселенной
тоже есть свои " нити " . Иоганн Кеплер в этом и видел
гармонию и красоту. Он считал, что мир пронизан невидимыми нитями. В этом
его убедила третья удивитель-
ная закономерность в движении планет. Квадраты периодов обращения планет
относятся как кубы их больших
полуосей (третий закон Кеплера). Большой полуосью называется половина
расстояния между двумя наиболее
удаленными друг от друга точками эллипса.
Но что это за невидимые нити? Более или менее это
стало понятно лишь в начале нашего века после работ
Альберта Эйнштейна по общей теории относительности.
Но еще в XVII веке Исаак Ньютон значительно прояснил
дело, заменив три закона Кеплера одним законом - законом всемирного
тяготения.
Движение в гравитационной воронке






