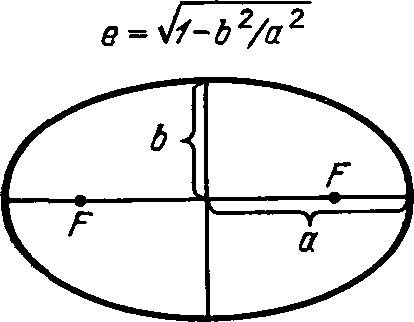Владимир Липунов
ГЛАВА I
Законы Кеплера
Движение в гравитационной воронке
Анализируя законы Кеплера, Ньютон пришел к выводу, что сила натяжения невидимых нитей,
связывающих удаленные тела, обратно пропорциональна
квадрату расстояния между ними. Эти нити он назвал
всемирным тяготением. Закон всемирного тяготения применим к любым телам независимо от цвета, вкуса, запаха и вообще химического состава. Универсальность тяготения объясняет, почему все планеты движутся по
одинаковым орбитам.
Кеплеру и Ньютону ≈ вообще человечеству ≈ сильно
повезло. Масса Солнца в сотни раз превышает массу всех
планет вместе взятых. Это означает, что обратное влияние планет на Солнце невелико и им можно пренебречь.
Поэтому движение планет вокруг Солнца выглядит достаточно просто. Однако на разгадывание эпициклов и диферентов человечеству понадобилось более тысячи лет.
Кто-то пошутил, что если бы человечество возникло на
планете в двойной звездной системе, где движение планет вообще не поддается формульному описанию, то оно
бы никогда не открыло закона всемирного тяготения;
следовательно, в таких звездных системах развитых цивилизаций не должно быть.
Совсем другое дело ≈ наша Солнечная система. Движение планет происходит в основном под действием Солнца. Взаимное притяжение планет очень мало. Такое
движение удобно рассматривать не на языке сил
(школьных знаний недостаточно, чтобы решить уравнения движения), а на энергетическом языке. Согласно закону Ньютона тела создают вокруг себя поле тяготения,
или гравитационное поле. Это поле характеризует потенциалU, физический смысл которого следующий.
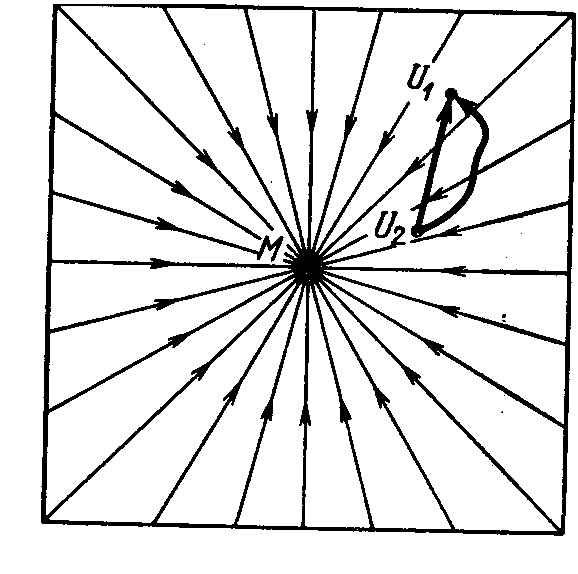
Пусть имеется тело массы
М (рис. 3). Чтобы измерить
его поле тяготения, необходимы так называемые пробные частицы ≈ тела, масса
которых настолько мала,
что их влияние на тело М
невелико. Обычно принимают массу пробных тел равной единице в той системе
единиц, в которой вы хотите
работать. Итак, возьмем
стим ее из точки 1 на бесконечность.
При этом нам
нужно приложить силу и,
преодолевая тяготение, совершить работу. Работа, выполняемая таким образом и
взятая с обратным знаком, называется потенциалом
гравитационного поля тела М. Наоборот, если из бесконечности падает частица, то работа, произведенная
гравитационным полем, и есть потенциал с обратным
знаком, ≈ U.
Сила гравитации зависит только от расстояния и направлена всегда по радиусу к телу М. Значит, и потенциал зависит только от расстояния до тела М. Работа,
которую нужно совершить, чтобы перенести пробную
массу из точки 2 в точку
1, равна разности потенциалов
U1 - U2 При свободном движении пробных частиц сохраняется их полная энергия, т. е. сумма кинетической
(К) и потенциальной энергии ((/): К + U == const. Потенциал точечного тела массы М имеет вид
U= - GM/r (1)
где
G ≈
постоянная тяготения, r ≈ расстояние от
тела
массы М. Значение постоянной тяготения удобнее всего
запомнить так: 1/G = 1,5 1010
кг с2/m3.
На рис. 4 качественно показан потенциал Солнца,
имеющий вид гиперболы. Вращая гиперболу вокруг оси
U, получим гравитационную
воронку. Полезное свойство
потенциала состоит в том,
что тело, ⌠помещенное■ в некоторой точке г, будет ⌠скатываться■ в область, где по-
тенциал меньше.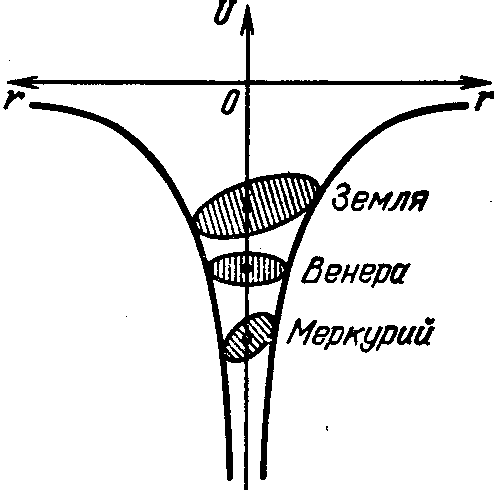
Планеты Солнечной системы ≈ те же пробные частицы. Теперь мы можем
сказать, что для Кеплера
и Ньютона планеты оказались именно теми пробными частицами, с помощью
которых они исследовали
свойства гравитационного
поля Солнца. (Мы же просто
живем на одной из таких пробных частиц под названием Земля.)
Как же происходит движение в гравитационной воронке? В координатах U (г) движение планет изображается кругами (если орбиты круговые) или овалами (не эллипсами !). Возникает вопрос: почему планеты не ⌠скатываются■ на дно воронки? Конечно, все дело в том, что
они обладают вращательным моментом (угловым моментом, обусловленным орбитальным движением). Движение планет происходит без трения, поэтому их вращательный момент исчезнуть не может. Но это не
единственно возможный тип движения в гравитационной воронке. Мы уже говорили о том, что если осторожно положить пробную частицу на склон воронки (а у нее везде склон), то она скатится к центру (упадет на Солнце). Наоборот, если сильно щелкнуть частичку, то она
может вообще улететь бесконечно далеко. В этом случае
говорят, что пробная частица получила скорость больше
второй космической. Мы наблюдаем движение только по
эллипсу потому, что все, что должно было улететь из Солнечной системы, давно улетело, а то, что должно было
упасть, давно упало.
Подробный анализ показывает, что все типы траекторий движения в гравитационной воронке можно получить с помощью конуса и плоскости. Пересекая конус
плоскостью, получим три типа кривых (рис. 5): 1) окружность или эллипс; 2) параболу; 3) гиперболу. Кривых
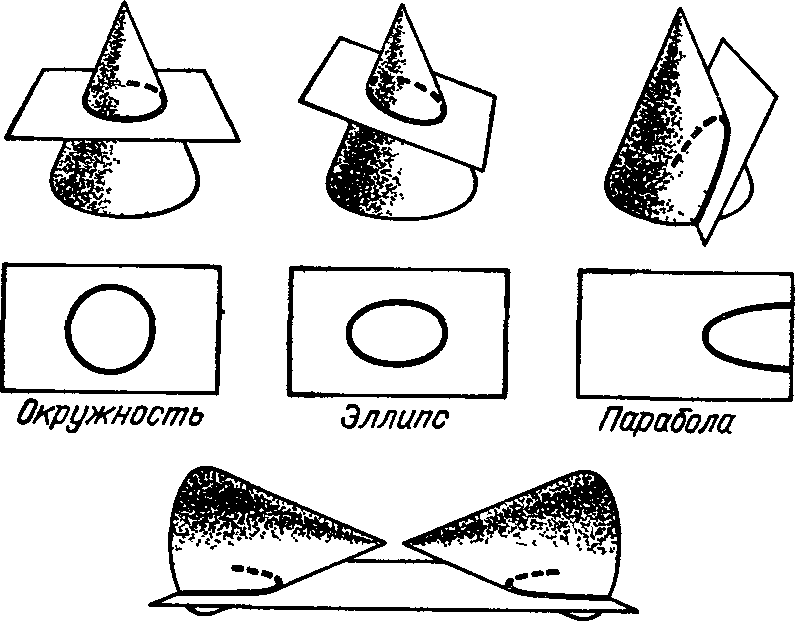
Гипербола
Рис. 5. Разные типы конических сечений
четыре, а типов три
(*). Это не случайно. Окружность
и эллипс соответствуют, замкнутому движению, для которого сумма кинетической и потенциальной энергий отрицательна. Парабола соответствует точному равенству
этой суммы нулю: К + U = 0. Наконец, гипербола соответствует полной положительной энергии. Например,
если бы в Солнечную систему прилетел межзвездный корабль, то он двигался бы по гиперболе, пока его обитатели не включили бы двигатели, чтобы выполнилось
неравенство К + U < 0. Это необходимое условие контакта.
Но вернемся к планетам. Важной характеристикой орбиты планеты ≈ эллипса ≈ является его эксцентриситет,
который показывает, насколько сжат эллипс (см. рис. 6).
Чем сильнее сжат эллипс, тем
больше его эксцентриситет и
тем ближе его значение к единице. Наоборот, у окружности
(несжатый эллипс) эксцентриситет равен нулю. У орбиты Земли
эксцентриситет е
= 0,017, поэтому она оказывается то ближе (зимой), то дальше (летом) от Солнца. Правда, эта разница расстояний очень невелика и не влияет существенно на смену времен года.
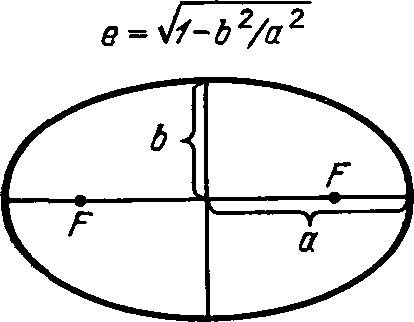
Первый закон Кеплера является следствием конкретного вида закона тяготения. Если бы сила тяготения изменялась не по закону обратных квадратов, то орбиты
пробных частиц были бы не эллипсами, и более того, они
не были бы замкнутыми. Однажды выброшенная из какой-либо точки частица никогда бы не повторила своего
пути дважды. Периодичность движения ≈ это уникальное
свойство сил, обратно пропорциональных квадрату расстояния
(**).
Второй закон Кеплера является следствием закона сохранения вращательного момента пробной частицы в поле силы тяжести точечной массы. Действительно, сила
тяготения всегда направлена по линии, соединяющей
пробную частицу и центральное тело. Вращательный момент определяется компонентой движения, перпендикулярной радиусу-вектору, и не может измениться из-за
силы тяготения. Это свойство относится не только
к тяготению, но и к любому центрально-симметричному полю сил.
Третий закон Кеплера можно записать в виде следую-
щей формулы, обозначив через Р период обращения
планеты вокруг Солнца:
a3/p2=GM/4 pi
Здесь
M = 2 ∙ 1030 кг - масса Солнца, а - большая полуось эллипса. Для круговых орбит этот закон может вывести любой школьник. Нужно только помнить, что для круга большая полуось - это просто его радиус.
Читатель может спросить, почему мы так подробно говорим о движении планет, хотя обещали рассказать о двойных звездных системах. В двойных системах массы звезд могут быть сравнимы, и тогда все это может оказаться неприменимым. Но удивительная вещь ≈ почти
все, о чем мы говорили выше, остается справедливым для двойных звезд.
(
*) Движение возможно и по прямой линии. Этот вырожденный
случай реализуется, если пробная частица не имеет вращательного момента. Полная энергия при этом может иметь любой знак.
(*
*) Таким свойством обладает еще движение тел в поле сил, прямо
пропорциональных расстоянию (вращение грузика на резинке).
Вокруг центра масс