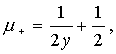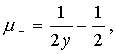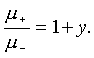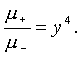Гравитационные линзы
А.Ф. Захаров
Государственный научный центр --
Институт теоретической и экспериментальной физики
Обсуждены основы действия природных телескопов, какими являются гравитационные линзы. Описана история возникновения этой концепции. На примере простейшей модели точечной гравитационной линзы рассмотрены возможные наблюдательные проявления гравитационной фокусировки.
The action basics of the natural telescopes which are gravitational lenses are discussed. The concept birth history was described. Using the simplest model of the point gravitational lens possible observational evidences are considered.
1.Историческое введение.
Известно, что распространение света в гравитационном поле описывается уравнениями общей теории относительности, тем не менее, отклонение лучей света от прямой линии обсуждалось вскоре после создания И. Ньютоном классической механики. Так, Ньютон в своей класической книге "Оптика" в 1704 г. сформулировал следующий вопрос:"Не действуют ли тела на свет на расстоянии, и не является ли это действие наиболее сильным на наименьшем расстоянии?" Т.о., можно говорить о том, что Ньютон сформулировал словами закон об отклонении луча света в гравитационном поле:
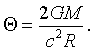 (1)
(1)
Точнее, Q
~ R-1, поскольку численные коэффициенты в то время не выписывались (не было общепринятой системы единиц). В своей классической книге "Математические основы натуральной философии" Ньютон показал, что под действием центростремительной силы, обратно пропорциональной квадрату расстояний до центра, тело движется по коническому сечению, фокус которого лежит в центре (напомним, что коническим сечением называется кривая, образованная при пересечении конической поверхности плоскосью, и коническим сечением в невырожденном случае могут быть только эллипс, гипербола или парабола). Поскольку при рассмотрении движения тела по гиперболической траектории Ньютоном были вычислены и полуоси, тем самым, ему был известен и угол между асимптотами. Т.о., учитывая то, что Ньютон достаточно часто не публиковал результаты, и форма представления им результатов также была весьма не простой, можно, по-видимому, утверждать, что формула (1) была Ньютону известна, более того, скорее всего, ему была известна соответствующая величина отклонения луча света вблизи поверхности Солнца, поскольку все необходимые значения констант ко времени опубликования "Начал" были известны. Действительно, первый директор Парижской обсерватории Дж. Кассини определил расстояние от Земли до Солнца в 1672 г., время обращения Земли вокруг Солнца определил датский астроном Тихо Браге с точностью до 1 с, а из третьего закона Кеплера, зная расстояние от Солнца до Земли и период обращения Земли, можно определить произведение
GMo
, т.к. T2/a3=4pi
2/(GMo
). Результаты датского астронома Ремера по измерению скорости света на основании изменения периода обращения спутника Юпитера Ио были опубликованы в 1677 г. Т.о., к 1687 г. (году опубликования "Начал") , все необходимые значения констант были известны, тем не менее в явном виде в научном наследии формулы (1) нет, не приведено также и значение для отклонения луча света вблизи поверхности Солнца, возможно, по причине слишком малого его значения - 0.87''. В качестве исторического казуса заметим (вслед за П.В. Блиохом и А.А. Минаковым), что если вычислить отклонение луча света вблизи поверхности Солнца, используя величину скорости света, определенную Ремером c = 2*1010 см/c, то для величины угла отклонения получится результат Q
=1.73'', что практически совпадает с результатом, полученным в рамках ОТО. Несмотря на то, что формула (1) Ньютону, по-видимому, была известна, первое упоминание о вычислении величины угла отклонения относится к 1784 году, когда соотношение (1) получил английский физик Генри Кавендиш, стимулированный перепиской со своим другом Джоном Мичеллом (тем самым, кто в 1783 г. за несколько лет до выходя в свет работы выдающегося французского физика и математика П. Лапласа рассмотрел звезды, гравитационное поле которых является столь сильным, что луч света не может покинуть поверхность звезды). Кавендиш не опубликовал свои вычисления, тем не менее, они были записаны "на отдельном листе бумаги".
В 1801 г. немецкий астроном Иоганн Георг фон Зольднер представил в Берлинский астрономический ежегодник статью об отклонении луча света в гравитационном поле звезды (статья опубликована в 1804 г.). Т.о., вывод формулы (1) впервые был опубликован Зольднером.
То, что эта замечательная работа Зольднера не была известна научному сообществу почти 120 лет (и то, что его имя чаще всего не упоминается в монографиях и учебниках по механике и теории гравитации), заставляет упомянуть некоторые страницы биографии этого ученого. Он родился 15 июля 1776 года в баварской деревне Георгенгофе, был сыном крестьянина, закончил один или два класса начальной школы в Файхтвагене и систематического школьного образования не получил. Лишь в 16 лет он брал частные уроки латинского и французского. Когда ему было 20 лет, его друзья предложили ему попробовать себя в качестве ученого в Ансбахе. То, что Зольднер был человеком с выдающимися способностями, вскоре подтвердилось, и представитель прусского правительство в Ансбахе предложил ему должность помощника директора Берлинской обсерватории И. Э. Боде, являвшегося иностранным почетным членом Петербургской Академии Наук. Публикации в ведущих научных журналах того времени, в частности, таких как Астрономический ежегодник, редактируемый Боде, принесли Зольднеру большую известность.Кроме исследования искривления света гравитирующим телом, Зольднер в своих статьях рассматривал движение звезд в Млечном Пути, проанализировал движение кометы, недавно открытой итальянским астрономом Дж. Пиацци.
Довольно интересной является статья Зольднера об анализе движения звезд в Млечном Пути, поскольку содержание статьи посвящено анализу так называемых невидимых тел Лапласа, т.е. тел, поле тяготения которых столь велико, что свет не может исходить от их поверхности. Впервые Лаплас упомянул о таких телах в первом и во втором издании книги "Изложение системы мира" (1796, 1799) (но по непонятной причине этот фрагмент был опущен в третьем (1808), четвертом (1813) и пятом изданиях). Одним из немногих, кто откликнулся на работу Лапласа, был Зольднер. Несмотря на то, что математический анализ в рассуждениях Лапласа был для Зольднера вне сомнений
, тем не менее, Зольднер не был согласен с гипотезой Лапласа о том, что скорость света является константой. По мнению Зольднера, процесс испускания света может быть весьма различным, и могут испускаться световые корпускулы с относительно малой скоростью и поэтому, в зависимости от химических и механических свойств материала, даже в том случае, если звезда достаточно мала, существует возможность того, что свет не может покинуть звезду. Зольднер рассмотрел следствия существования большой массы в центре больших звездных систем таких, как Млечный Путь. То, что такие звездные
системы существуют, не вызывало сомнений после работ немецких ученых И. Канта и И.Г. Ламберта и английского астронома У. Гершеля. Тем не менее, вопрос о том, описывается ли движение звезд действием массивного тела в центре Млечного Пути, проанализирован Зольднером. Он пришел к выводу, что такого центрального тела нет, поскольку движение звезд вокруг этого тела должно быть достаточно быстрым, что не было заметно из наблюдений. Зольднер пришел к этому заключению, исходя из вычисления относительных скоростей звезд ближе и дальше от центра однородного распределения звезд, образующих сильно сжатый вдоль одной из осей сфероид. Он предположил, что все видимые звезды так близки к центру, что они находятся на расстоянии не более 1/10 размера Млечного Пути, но даже в этом случае угловые скорости звезд существенно различаются. В результате он пришел к выводу, что тем самым не подтверждается гипотеза о существовании массивного тела (даже в виде невидимых звезд Лапласа).
В 1804 появилась первая работа Зольднера по геодезии, где обсуждался шведский проект измерения градуса Земной окружности, а также его собственное подобное предложение, связанное с проведением змерений в экваториальной Африке. Несомненно, в связи с появлением этих работ он к 1805 г. уже трижды получает предложение занять должность директора Обсерватории Московского Университета. В то же время его друзья, желавшие сохранить его способности для Германии, способствовали получению им должности
директора прусского геодезического управления в округе Ансбах. Спустя три года Зольднер занял должность директора баварского геодезического управления. Но быстрое продвижение по службе вызвало зависть его коллег. Через год после занятия Зольднером этой должности Мюнхенская Академия Наук отозвала его с этой должности, поскольку его имя упоминалось в связи с обвинениями в плагиате. Обвинение касалось оригинальности опубликованной в 1813 году в Ежегоднике Боде знаменитой работы Зольднера об увеличении точности определения азимута. Вследствие детального разбирательства обвинения имя Зольднера не только было полностью реабилитировано, но и его обвинитель, Феликс Зейффер, член Мюнхенской Академии Наук и директор обсерватории Мюнхенской Академии, был смещен с поста директора, и этот пост был занят Зольднером, что позволило ему заняться созданием новой обсерватории. В 1818 г. обсерватория в Боденхаузене близ Мюнхена была построена и, благодаря компетенции Зольднера, была оснащена наилучшими в то время инструментами. Инструменты для обсерватории были изготовлены в мастерской Й. Фраунгофера (впоследствии Зольднер рекомендовал Фраунгофера в члены Мюнхенской Академии Наук). В 1825 г. Зольднер получил дворянский титул от короля Баварии и от короля Франции, а также стал по рекомендации более молодого У. Гершеля членом-корреспондентом Королевского Астрономического Общества в Лондоне. Между тем, вследствие болезни печени, Зольднер вынужден был поручить проведение наблюдений, связанных с задачей исследования движения звезд, своему заместителю Йоханну Ламонту. Несмотря на то, что эта тема была предметом первой публикации Зольднера, он достаточно долго не публиковал свои работы по астрономии. Только в 1811 г. он опубликовал фрагмент своего частного письма под названием "О теории света, тепла и о работе из интегрального исчисления", где было предложено рассматривать свет как четвертое состояние вещества, отличное от твердого, жидкого и газообразного. В дальнейшем Зольднер провел достаточно много исследований, полезных для геодезии и астрономии. Так, в серии В.Ф. Оствальда "Klassiker der Naturwissenschaften" ("Классики точных наук") была опубликована работа Зольднера о решении треугольников на достаточно плоских сфероидах, например, таких, как Земля. Суть статьи состоит в методе вычислении длин дуг с точностью не ниже 1 см при длине дуги порядка нескольких километров вместо того, чтобы заменять дуги хордами.
18 мая 1833 г. он умер на посту директора этой обсерватории. После его смерти на пост директора обсерватории предлагался Франц Гротенхойзен, который был профессором астрономии в Мюнхенском Университете, но довольно слабо владел математическим аппаратом. Кандидатура Гротенхойзена вызвала беспокойство у Ф.В. Шеллинга, который был президентом Мюнхенской Академии, куратором естественных наук и сторонником точных методов в науке. Благодаря рекомендациям выдающихся немецких ученых К.Ф. Гаусса и Ф.В. Бесселя, пост директора занял Йохан Ламонт, который продолжил на этом посту лидерство Зольднера в точности измерений и использовании новых математических методов в астрономии и геодезии.
Но, несмотря на достаточно высокое положение Зольднера в науке, его работа об отклонении света была практически забыта. Ее значение стало ясно научной общественности лишь после появления работ Эйнштейна.
В 1911 г. А. Эйнштейн получил в рамках специальной теории относительности (СТО) то же самое значение для угла отклонения луча света вблизи поверхности Солнца (что и вычисляемое с использованием формулы (1). К началу XX века астрономы уже могли измерить подобные углы отклонения. Действительно, в 20-х годах XIX века, благодаря работам Фраунгофера, были созданы телескопы, с помощью которых немецкий астроном и математик Ф.В. Бессель и русский астроном и геодезист В.Я. Струве измерили звездные параллаксы, которые много меньше 1''. Группа астрономов из Берлинской обсерватории во главе с Э. Фрейндлихом заинтересовалась предсказаниями Эйнштейна и собралась провести измерения во время предстоящего полного солнечного затмения в Крыму в августе 1914 г. Астрономы уже были в Крыму, но началась I мировая война, они были арестованы и вскоре обменены на граждан России, арестованных в Германии. Т.о., к счастью для Эйнштейна, наблюдения не были проведены. В 1915 в рамках общей теории относительности А. Эйнштейн получил удвоенное значение для угла отклонения
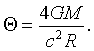 (2)
(2)
Вскоре после окончания I мировой войны группой английских астрономов во главе с А. Эддингтоном были проведены наблюдения отклонения луча света во время полного солнечного затмения 29 мая 1919 г. Как сообщалось в публикации результатов экспедиции, ее задачей был выбор одной из трех
возможностей: 1) гравитационное поле Солнца не оказывает влияния на траекторию луча света; 2) гравитационное поле Солнца действует на световой луч как на обычное вещество, если закон тяготения носит ньютоновский характер, что приводит к кажущемуся смещению во внешнем направлении звезды у края солнечного диска, равному 0.87''; 3) Ход луча согласуется с ОТО, что приводит к кажущемуся смещению во внешнем направлении звезды у края диска, равному 1.75''.
При формулировке задач экспедиции было замечено, что "смещение 2) впервые было вычислено проф. А.Эйнштейном на основе принципа относительности". Результаты наблюдений были получены в двух географических точках: в Собрале и на Принсипи. В Собрале было получено среднее отклонение
1.98'' +/- 0.12'', на Принсипи 1.61''+/- 0.30''.
Тем не менее, в Собрале были получены пластины, давшие отклонение 0.93''. Эти результаты были отброшены, поскольку случайная ошибка была слишком велика. Т. о., в результате наблюдений приведено убедительное подтверждение предсказаний А. Эйнштейна. Немецкий нобелевский лауреат Ф. Ленард в 1921 г., заметив, что впервые формула (1) получена в работе Зольднера, и привел в своей статье фрагмент этой работы и аргументацию того, что результаты согласуются с предсказанием отклонения 0.87''. Тем не менее, последующие наблюдения с помощью методов радиоинтер-ферометрии подтвердили предсказания Эйнштейна с точностью выше 1%.
По-видимому, первый, кто использовал термин "линза" в контексте отклонения луча света гравитацией, был английский физик О. Лодж, который в 1919 г., однако, отметил, что " гравитационное поле действует, как линза, но не имеет фокусной длины".
Петербургский физик О. Хвольсон в 1924 г. опубликовал короткую заметку, в которой заметил, что в случае, когда рассматривается отклонение луча света фоновой звезды звездой--линзой, возможно возникновение второго изображения фоновой звезды, но угол между двумя изображениями столь мал, что эти изображения нельзя разрешить с помощью наземного телескопа. В случае, когда наблюдатель линза и источник находятся на одной прямой, возникает изображение типа кольца. По утверждению американского астронома Барноти, эти кольца, называемые сейчас "кольцами Эйнштейна", должны называться "кольцами Хвольсона", а крупнейшие специалисты в теории гравитационных линз П. Шнайдер, Ю. Элерс и Э. Фалько приводят по этому поводу пословицу "the biggest cat gets all the milk". В настоящее время в основном используется термин "кольцо Эйнштейна" и значительно реже "кольцо Хвольсона--Эйнштейна".
Следует заметить, чтозначительно большая популярность работы Эйнштейна связана не только со значительно большей его известностью по сравнению с Хвольсоном, но и со значительно большей популярностью журнала "Science" по сравнению с потсдамским астрономическим журналом "Astronomische Nachrichten". В 1936 г. А. Эйнштейн опубликовал заметку, где по просьбе чешского инженера Мандла рассмотрел линзообразное действие звезды на фоновую звезду, в частности, появление кольца в случае, если наблюдатель, линза и источник находятся на одной прямой ( в этом случае появляется "кольцо Эйнштейна"). А. Эйнштейн заметил, что "конечно нельзя надеяться на то, что удастся прямо наблюдать это явление". Ниже мы постараемся обсудить это замечание А. Эйнштейна. Кроме того, в данной заметке был вычислен коэффициент усиления источника гравитационной линзой. Следует заметить, что и Хвольсон, и Эйнштейн считали, что не может наблюдаться эффект гравитационной линзы
( в смысле наблюдения двойной звезды или "кольца Эйнштейна"), поскольку они рассматривали случай, когда и источник, и гравитационная линза являются звездами.
Однако немецкий астроном Ф. Цвикки в 1937 г. пришел к выводу, что эффект может быть наблюдаем в случае, если источником является туманность, а гравитационной линзой--галактика. Приведем цитату из работы Цвикки: "Прошлым летом доктор В.К. Зворыкин (которому подобная идея была сообщена Мандлом), заметил мне о возможности образования изображения как результат действия гравитационных полей. Как следствие, я провел некоторые вычисления. Внегалактические туманности имеют гораздо больше шансов, чем звезды, для наблюдения эффектов гравитационной линзы". Эта цитата может быть образцом стиля научных работ более чем полвека назад со ссылками на чужие, даже не до конца определенно сформулированные идеи. Для того, чтобы убедится в том, что это не единичный пример, можно привести цитату из работы А. Эйнштейна: "Некоторое время тому назад меня посетил Р. Мандл и попросил опубликовать результаты небольшого расчета, который я провел по его просьбе. Уступая его желанию, я решил опубликовать эту заметку". Цитата из работы Цвикки демонстрирует самое широкое влияние на развитие мировой науки широкого влияния русской научной школы, в том числе, блестящих представителей первой русской эмиграции, таких, как В.К. Зворыкин, технические открытия которого фактически позволяют назвать его "отцом" телевидения. Насколько плодотворным было замечание Зворыкина и, безусловно, последующий анализ Цвикки, стало ясным спустя более сорока лет. Действительно, когда английскими астрономами Д. Волшем и др. в 1979 г. (рис. 1) была обнаружена первая гравитационная линза при наблюдении двойного квазара QSO 0957+16 A,B
(
z примерно равно 1.4, угловое
расстояние между изображениями порядка 6''), и гравитационной линзой являлась галактика (zd равно 0.36), то стало возможным говорить о том, что предсказание Цвикки подтвердилось.
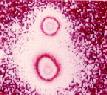
Рис. 1. Изображение первой гравитационной линзы QSO 0957+16 A и B, взятое из галереи гравитационных линзы профессора Ж. Сюрдеча, расположенной на интернет-сайте http://vela.astro.ulg.ac.be.
В настоящее время известно 10 установленных объектов, связываемых с гравитационными линзами, и 15 объектов, предложенных для дальнейшей проверки, кроме того, 5 радиодуг, связываемых с гравитационными линзами. С 1979 г. количество опубликованных работ, посвященных гравитационным линзам, столь велико, что невозможно коротко упомянуть даже самые значительные, однако можно отметить обнаружение гравитационного микролинзирования в 1993 году (т.е. характерное изменение светимости фоновой звезды, обусловленное действием гравитационной линзы, являющейся невидимым объектом звездной массы), а также появление первых алгоритмов для восстановления поверхностной плотности скрытого вещества по наблюдаемому искажению формы далеких галактик, т.е. проявление, так называемого слабого гравитационного линзирования, когда гравитационная фокусировка приводит не к появлению кратных изображений исходных объектов, а только к искажению их формы.
2. Вывод формулы Зольднера.
Выберем систему координат таким образом, что гравитирующий центр лежит в начале координат и пусть из точки S в направлении, параллельном оси абсцис испускается луч света (рис. 2.).
Через время
t луч света будет находится в точке A. Введем следующие обозначения: DM = r, DP = p, Ð
ADP = j
.
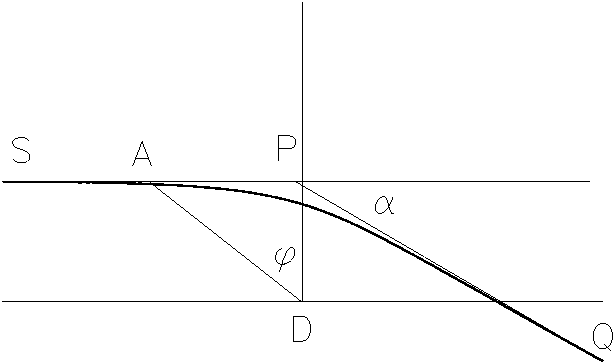
Рис. 2. Искривление траектории луча света гравитирующим телом. Луч, испускаемый из точки S, текущее положение луча света характеризуется точкой A, которой соответствует угол j
. OAQ -- траектория луча света в ньютоновском поле (гипербола).
Предположим, что фотон обладает энергией
E = hn
и массой m=E/c2, где h=6,626×
10-27 эрг*c--постоянная Планка, n
--частота фотона, c=2,997 см/c скорость света. Тогда согласно закону всемирного тяготения, изменение проекции вектора скорости на ось Oy, определяется соотношением
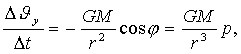 (3)
(3)
где
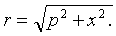
Интервал временени связан со значением интервала по оси
Ox следующим образом
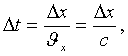 (4)
(4)
предполагая, что
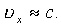
Если ввести замену переменной x следующим образом:
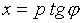 , то
, то
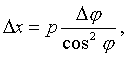 (5)
(5)
поскольку
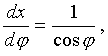 то
то 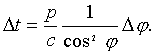
Тогда
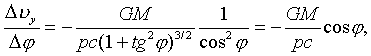 (6)
(6)
В этом случае, полное изменение может быть вычислено с использованием
определенного интеграла
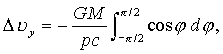 (7)
(7)
Поскольку
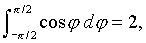 (8)
(8)
то
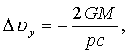 (9)
(9)
а угол отклонения характеризуется соотношением
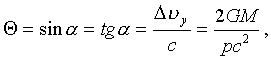 (10)
(10)
Вычислим угол отклонения луча света вблизи поверхности Солнца. В этом случае радиус Солнца R¤
=6.96×
1010 cм, масса Солнца M¤
=1.989×
1033 г, значение гравитационной постоянной равно G=6.673×
10-8 cм3/(г×
c2), c=2.997×
1010 см/c и угол отклонения равен 0.875''. Зольднером было получено значение 0.84''. Расхождение в результате связано с уточнением значений констант, используемых для вычислений по формуле Зольднера.
3. Точечная гравитационная линза
Рассмотрим основные понятия теории гравитационных линз на примере точечной гравитационной линзы. Будем считать, что свет движется не по кривой, похожей на гиперболу, а по асимптотам этой кривой. Ясно также, что идеальная гравитационная линза является ахроматической, но в реальной ситуации разные части источника могут иметь различный цвет, и, тем самым, могут возникнуть различные эффекты, связанные с цветом. Итак, рассмотрим идеальную точечную гравитационную линзу (рис. 3).
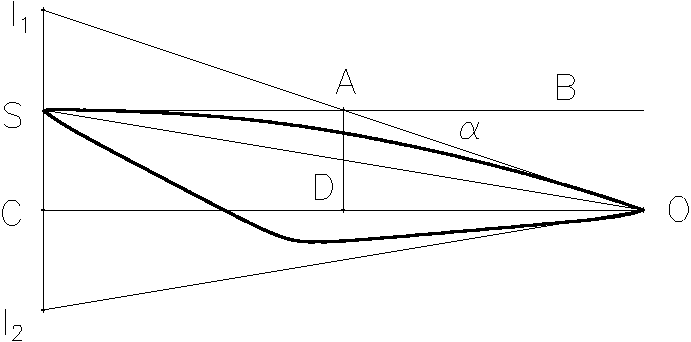
Рис. 3.
Геометрия гравитационной линзы.
Пусть расстояние между источником и наблюдателем
- Ds, расстояние между гравитационной линзой и наблюдателем -Dd , расстояние между гравитационной линзой и источником - Dds. Проведем через точку, в которой находится гравитационная линза, плоскость (плоскость линзы), перпендикулярную прямой, соединяющей линзу и наблюдателя. Аналогично через источник проведем плоскость, параллельную плоскостилинзы, плоскость источника.
Пусть векторы h
, x
определяют координаты в плоскости источника и в плоскости линзы соответственно, тогда из подобия треугольников D
OAD и D
OI1C получаем, используя эйнштеновскую формулу для отклонения луча света (2)
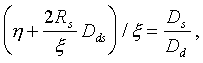 (11)
(11)
Тогда уравнение гравитационной линзы имеет следующий вид:
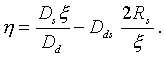 (12)
(12)
Приравнивая к нулю правую часть уравнения (12), получим условия, когда источник, линза, и наблюдатель находятся на одной прямой (h
=0). Соответствующее значение
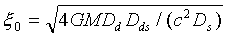 называется радиусом Эйнштейна--Хвольсона. Можно вычислить также угол Эйнштейна--Хвольсона q
0 = x
0/Dd. Вычислим значение угла q
0 для типичной ситуации, когда гравитационной линзой и источником являются звезды, и когда источником является квазар, а гравитационной линзой галактика. Напомним, что квазары (от английского слова quasar = quasistellar radiosource) - это мощные внегалактические источники электромагнитного излучения, имеющие на фотографиях звездообразный вид. Природа мощного энерговыделения квазаров в настоящее время до конца неизвестна, однако обычно предполагается, что это энерговыделение связано с астрофизическими процессами в окрестности сверхмассивных черных дыр. Будем считать, что Ds ¯
Dd, тогда
называется радиусом Эйнштейна--Хвольсона. Можно вычислить также угол Эйнштейна--Хвольсона q
0 = x
0/Dd. Вычислим значение угла q
0 для типичной ситуации, когда гравитационной линзой и источником являются звезды, и когда источником является квазар, а гравитационной линзой галактика. Напомним, что квазары (от английского слова quasar = quasistellar radiosource) - это мощные внегалактические источники электромагнитного излучения, имеющие на фотографиях звездообразный вид. Природа мощного энерговыделения квазаров в настоящее время до конца неизвестна, однако обычно предполагается, что это энерговыделение связано с астрофизическими процессами в окрестности сверхмассивных черных дыр. Будем считать, что Ds ¯
Dd, тогда
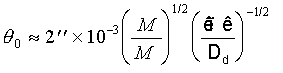 .
.
Напомним, что в астрономии расстояния довольно часто измеряются в парсеках, сокращенно пк, и 1 парсек = 1 пк =3,26 св. года = 206265 а.е.= 3×
1016 м -- это расстояние, соответствующее годичному параллаксу в одну секунду дуги или, иными словами, расстояние, с которого отрезок прямой соединяющий Землю и Солнце виден под углом 1'' (световой год (сокращенно св.год) -- расстояние, которое проходит луч света за один год (св. год = 9, 46×
1015 м); астрономическая единица (сокращенно а.е.) -- среднее расстояние от Земли до Солнца (1 а.е. = 1, 49×
1011 м)). Если гравитационная линза - одна из ближайших галактик с массой M=1012 M¤
, удаленная на расстояние Dd = 100 кпк, то q
0 »
200''. Если линза находится на расстоянии 1 кпк от наблюдателя (возможно, в нашей Галактике) и имеет массу порядка солнечной M = M¤
, то q
0 »
2''´
10-3. Этот случай гравитационной фокусировки называется гравитационным микролинзированием. Поскольку разрешающая способность наземных оптических ограничена долями угловой секунды, то в этом случае невозможно разрешить эти изображения с помощью наземных оптических телескопов (однако возможно, что в будущем
Запишем уравнение линзы, отнормировав угловые переменные на угол Эйнштейна--Хвольсона, а именно, использовав переменные
x
=x
/x
0, y=Dsh
/(x
0Dd), a
=Q
DdsDd/(Dsx
0), (13)
Тогда уравнение гравитационной линзы имеет вид:
y=x-a
(x)
или y=x-x/x2. (14)
Решая это уравнение относительно
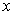 , получаем
, получаем
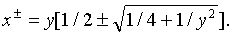 (15)
(15)
Отсюда без труда может быть вычислено расстояние между изображениями источника:
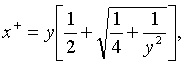
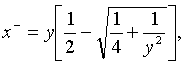
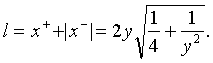 (16)
(16)
В случае, если
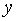 "1, то l »
2, т.е. расстояние между изображениями порядка диаметра Эйнштейна. Легко понять, почему круглый источник имеет изображения, вытянутые вдоль окружности с центром в начале координат. Действительно рассмотрим источник, расположенный недалеко от начала координат
"1, то l »
2, т.е. расстояние между изображениями порядка диаметра Эйнштейна. Легко понять, почему круглый источник имеет изображения, вытянутые вдоль окружности с центром в начале координат. Действительно рассмотрим источник, расположенный недалеко от начала координат 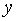 "1. Тогда его изображения находятся вблизи окружности Эйнштейна (x+ вне круга, x- внутри). Дуга окружности с центром в начале координат и проходящая через точки пересечения диаметра источника, перпендикулярного оси абсцисс, отображается в два сильно вытянутые изображения (примерно в 1/y раз). Рассмотрим, как изменяется при преобразовании гравитационной линзой размер источника в радиальном направлении, в предположении, что источник находится на оси абсцисс (это предположение можно сделать без ограничения общности). При
"1. Тогда его изображения находятся вблизи окружности Эйнштейна (x+ вне круга, x- внутри). Дуга окружности с центром в начале координат и проходящая через точки пересечения диаметра источника, перпендикулярного оси абсцисс, отображается в два сильно вытянутые изображения (примерно в 1/y раз). Рассмотрим, как изменяется при преобразовании гравитационной линзой размер источника в радиальном направлении, в предположении, что источник находится на оси абсцисс (это предположение можно сделать без ограничения общности). При 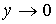 (малых значениях y)
(малых значениях y)
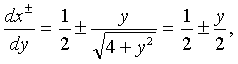 (17)
(17)
поэтому ясно, что изображения сужаются в этом направлении примерно в два раза по сравнению с источником.
В случае, если точечный источник находится на оси симметрии, изображение является кольцом, которое впервые обсуждалось в работе Хвольсона, опубликованной в 1924 г., а затем в заметке Эйнштейна, опубликованной в 1936 г. Следует заметить, что выше цитировалось утверждение Эйнштейна о том, что маловероятно наблюдать подобное кольцо. Более точно было бы говорить в данном случае о том, что наблюдать подобное кольцо в случае точечного источника невозможно, т.к. поскольку при малом изменении параметров кольцо исчезает и появляется два точечных изображения. В случае, если источник не точечный, тогда появление кольца в принципе возможно, хотя и менее вероятно, чем появление дуг.
Коэффициент усиления
Определим коэффициент усиления гравитационных линз. Следует заметить, что вследствие того, что коэффициент усиления изображения больше 1 (в некоторых случаях), рассматриваемое искривление света гравитирующим телом может называться гравитационным линзированием (гравитационной фокусировкой), а гравитирующее тело -- гравитационной линзой.
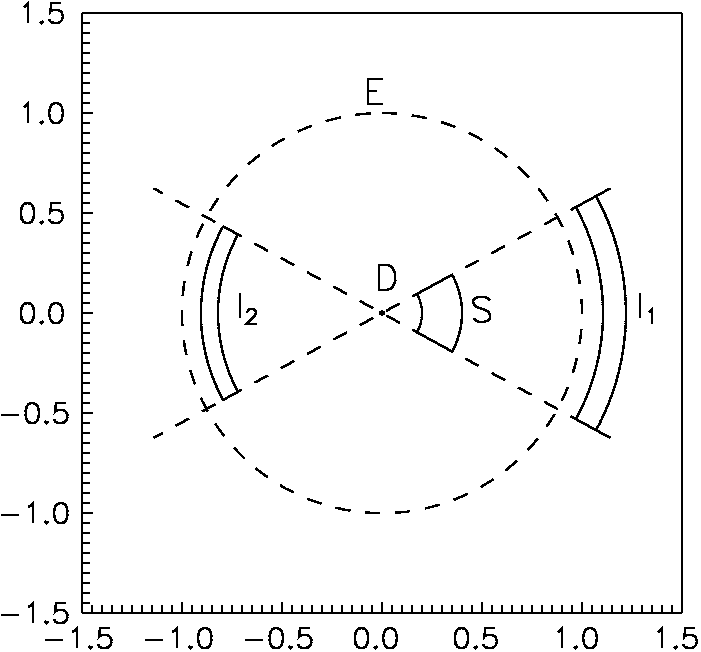
Рис. 4.
Формирование гравитационной линзой изображений источника, имеющего форму элемента кольца.
Введем важное понятие, определяющее гравитационную фокусировку, так называемый, коэффициент усиления гравитационной линзы. Он определяется отношением площади на небесной сфере изображения к площади источника. Предположим, для простоты рассуждения, что достаточно малый источник представляет собой небольшой элемент кольца радиус которого меняется в пределах от
y до y + D
y, а угол в пределах от 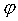 до
до 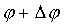 (рис. 4). В случае, если
(рис. 4). В случае, если 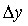 и
и 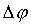 -- достаточно малы, то можно считать элемент кольца прямоугольником, его стороны соответственно равны
-- достаточно малы, то можно считать элемент кольца прямоугольником, его стороны соответственно равны 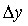 (для стороны, лежащей на радиусе) и
(для стороны, лежащей на радиусе) и 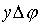 (для стороны, лежащей на окружности). Тем самым, площадь элемента кольца равна
(для стороны, лежащей на окружности). Тем самым, площадь элемента кольца равна
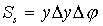 (18)
(18)
Если мы рассмотрим изображение источника, которому соответствует решение
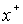 уравнения гравитационной линзы, то из соображений симметрии ясно, что это изображение также является элементом кольца, радиус которого меняется от
уравнения гравитационной линзы, то из соображений симметрии ясно, что это изображение также является элементом кольца, радиус которого меняется от 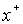 до
до 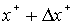 , а угол в пределах от
, а угол в пределах от 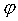 до
до 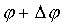 , где
, где
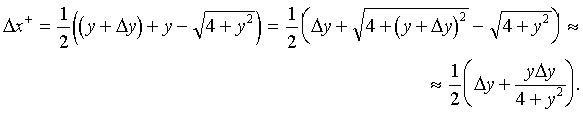 (19)
(19)
Поскольку изображение при малых значениях
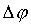 и
и 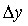 (а следовательно и малых
(а следовательно и малых 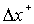 ), также как и источник можно считать прямоугольником, то площадь изображения равна
), также как и источник можно считать прямоугольником, то площадь изображения равна
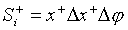 . (20)
. (20)
Коэффициент усиления гравитационной линзы характеризует то, во сколько раз площадь изображения на небесной сфере больше площади источника, т.е.
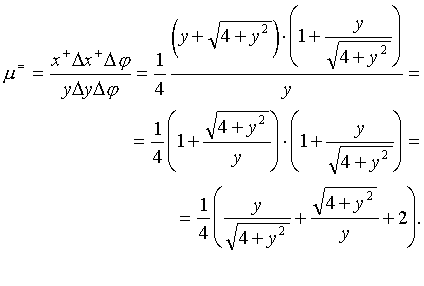 (21)
(21)
Если мы рассмотрим изображение источника, которому соответствует решение
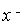 уравнения гравитационной линзы, то из соображений симметрии ясно, что это изображение также является элементом кольца, радиус которого меняется от
уравнения гравитационной линзы, то из соображений симметрии ясно, что это изображение также является элементом кольца, радиус которого меняется от 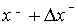 , а угол в пределах от
, а угол в пределах от 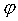 до
до 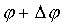 . Аналогично рассуждениям, приведенным выше, коэффициент усиления для этого изображения равен
. Аналогично рассуждениям, приведенным выше, коэффициент усиления для этого изображения равен
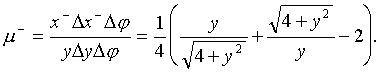 (22)
(22)
Тогда коэффициент усиления, соответствующий двум изображениям, равен
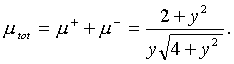 (23)
(23)
Нетрудно видеть, что
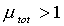 , тем самым, в любом случае влияние гравитационной линзы приводит к усилению изображений, и поэтому влияние гравитационного поля приводит к гравитационной фокусировке, которое называется гравитационным линзированием. При малых значениях y (y ®
0) имеем следующее выражение для коэффициента усиления
, тем самым, в любом случае влияние гравитационной линзы приводит к усилению изображений, и поэтому влияние гравитационного поля приводит к гравитационной фокусировке, которое называется гравитационным линзированием. При малых значениях y (y ®
0) имеем следующее выражение для коэффициента усиления
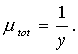 (24)
(24)
Ясно, что отношение коэффициентов усиления изображений определяется следующим соотношением
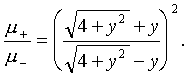 (25)
(25)
Рассмотрим предельные значения для величин
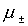 и их отношения при малом отклонении источника от оси симметрии y®
0
и их отношения при малом отклонении источника от оси симметрии y®
0
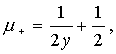
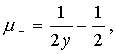
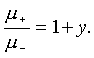
В пределе
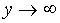 получим
получим
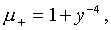
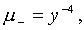
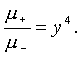
Следует заметить, что модель точечной гравитационной линзы (с помощью которой можно проследить возникновение двойного изображения), хотя и является весьма поучительной, но, по-видимому, использовать ее следует с большой осторожностью, поскольку в реальных ситуациях или угловое расстояние между изображениями слишком мал (мал угол Эйнштейна как в наблюдаемых случаях микролинзирования), или линза имеет большую массу и большие размеры, так что ее нельзя рассматривать как материальную точку (как в первых наблюдаемых примерах гравитационных линз).
Заключение
В небольшой статье невозможно рассказать об всех аспектах теории гравитационных линз и их наблюдений. Как уже было сказано ранее, обнаружить гравитационные линзы можно по наблюдениям пар квазаров, которые имеют похожие спектры и временную переменность компонентов, отличающуюся лишь временным сдвигом, который может принимать значения для различных пар изображений от нескольких дней до нескольких лет.
Гравитационные линзы являются и важным инструментом астрономических исследований. Так например, с их помощью можно получить независимую от других методов исследований оценку величины постоянной Хаббла, характеризующей в зависимости от расстояний скорости убегания от нас астрономических объектов, находящихся на космологических расстояниях; оценить массы гравитационных линз, большая часть которой испускает слишком мало электромагнитного излучения для того, чтобы быть обнаружена с помощью стандартных астрономических методов; с помощью методов так называемого слабого гравитационного линзирования восстановить распределение поверхностной плотности удаленных скоплений галактик по наблюдаемому изменению формы удаленных фоновых галактик; по характерному изменению кривой блеска фоновой звезды, или говоря иными словами, по характерному изменению ее наблюдаемой светимости, можно обнаружить невидимые объекты с массами порядка солнечной, т.е. обнаружить события, связанные с проявлением событий так называемого микролинзирования.
Заметим в заключение, что цветные изображения гравитационных линз, собранные известным бельгийским астрономом-исследователем гравитационных линз проф. Ж. Сюрдеча, можно найти с помощью системы Internet на WWW-сайте http://vela.astro.ulg.ac.be, так например одна из наиболее известных систем изображений квазара, связанных с проявлением эффекта гравитационного линзирования, показана на рис. 5.
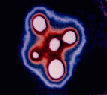
Рис. 5.
Изображение квазара QSO 2237 A, B, C, D ("крест Эйнштейна"), взятое из галереи гравитационных линзы профессора Ж. Сюрдеча, расположенной на интернет-сайте http://vela.astro.ulg.ac.be.
рекомендуемаЯ литература
1. Захаров А.Ф. Гравитационные линзы и микролинзы. М.: Янус, 1997.
Александр Федорович Захаров, доктор физико-математических наук, ведущий научный сотрудник Государственного Научного Центра -- Института теоретической и экспериментальной физики. Область научных интересов -- релятивистская астрофизика: гравитационные линзы, черные дыры, гравитационные волны. Автор более 100 научных работ и одной монографии.



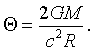 (1)
(1)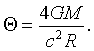 (2)
(2)

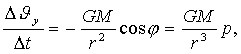 (3)
(3)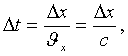 (4)
(4)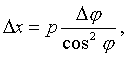 (5)
(5)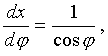 то
то 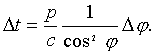
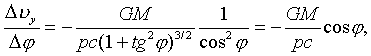 (6)
(6)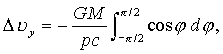 (7)
(7)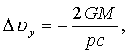 (9)
(9)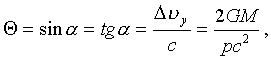 (10)
(10)
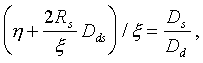 (11)
(11)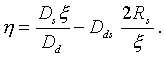 (12)
(12)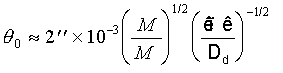 .
.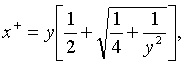
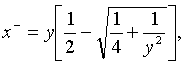
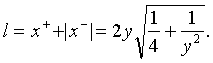 (16)
(16)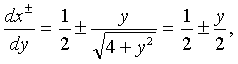 (17)
(17)
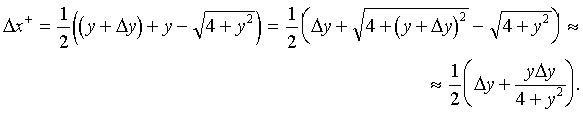 (19)
(19)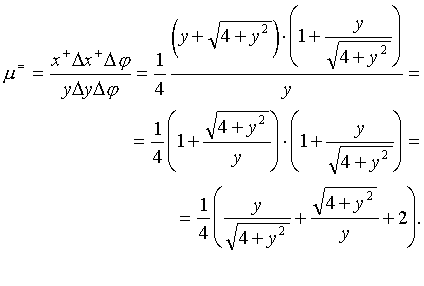 (21)
(21)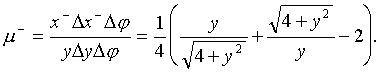 (22)
(22)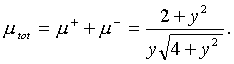 (23)
(23)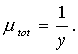 (24)
(24)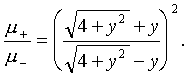 (25)
(25)