Предыдущее
На практике спектр звезды получают следующим образом. В
фокусе телескопа помещают спектрограф прибор, который работает наподобие
призмы,
но гораздо лучше.
При получении спектра телескоп нужен для того,
чтобы собрать как можно больше света от слабой
звезды. При этом спектр либо снимают на фотопластин-
ку, либо записывают через преобразователь в ЭВМ. Полученный спектр звезды
сравнивают с лабораторным
спектром какого-либо химического элемента.
Снимая спектр в различные моменты времени, на разных
орбитальных фазах, можно определить скорость
движения двойных звезд. Зависимость скорости от фазы называют кривой лучевых скоростей. При движении
звезды по орбите периодически меняется проекция скорости звезды на луч
зрения. Заметьте, что у компонент
двойной эти изменения происходят строго в противофазе. На спектрах видно,
как линии компонент ходят
в противофазе (рис. 25).
Рассмотрим простой случай круговых орбит. Пусть
луч зрения находится в плоскости двойной (рис. 25).
К ноблюдателю
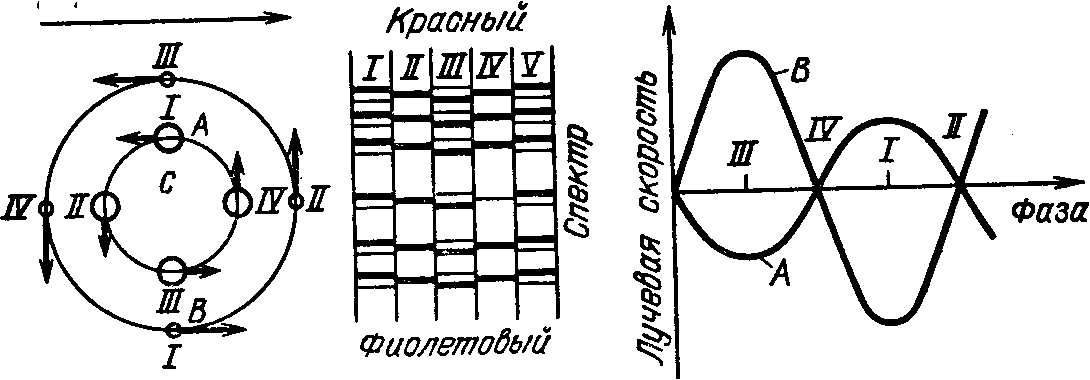
Рис.
25.
Периодическое хождение линий в спектре двойной (римскими цифрами показано соответствие положений звезд и спектральных
линий)
Пусть звезда
1 и
более горячая, и более массивная. В момент первичного минимума проекция
орбитальной скорости каждой звезды на луч зрения равна нулю. Затем
звезда 1 начинает приближаться, а звезда 2, наоборот,
удаляться от нас. Приближение характеризуется отрицательной скоростью, а удаление положительной.
Кривые лучевых скоростей представляют собой две синусоиды в противофазе.
Амплитуды синусоид равны орбитальным скоростям. Но иногда синусоиды
пересекаются не на оси абсцисс.
Все дело в том, что система движется относительно
нас как целое. Скорость, при которой пересекаются
кривые лучевых скоростей компонент, называется гамма-скоростью. Ясно, что
гамма-скорость это проекция
скорости центра масс двойной на луч зрения.
Что можно сказать о параметрах двойной, зная кривую
лучевых скоростей? Прежде всего, она позволяет
определить абсолютные размеры орбиты двойной ведь
нам известны скорость движения по орбите и период
двойной. Можно сказать, что длина волны квантов света,
излучаемых атомами, оказалась той самой линейкой,
с помощью которой удалось измерить размер двойной
системы. Зная размер большой полуоси и период, с помощью третьего закона Кеплера
(формула (2)) можно
найти сумму масс двойной. А можно ли найти массы
звезд по отдельности? Можно. Вспомним, что отношение орбитальных скоростей
звезд равно обратному отношению их масс. Значит, зная отношение амплитуд
кривых лучевых скоростей, мы сможем узнать отношение
масс звезд.
Итак, анализируя кривые лучевых скоростей и кривые
блеска, можно найти не только размеры орбиты двойной, но и массы и размеры
звезд. Конечно, это возможно
при условии, что в спектре видны линии обеих звезд
и что двойная система, видна с ребра. В противном случае обычно привлекают
дополнительную (косвенную) информацию и все же оценивают параметры звезд,
входящих
в двойную систему.
Среди двойных звезд часто бывает так, что в спектре
видны линии лишь одной из звезд более яркой. В этом
случае мы имеем только одну кривую лучевых скоростей,
а именно кривую лучевых скоростей более яркой звезды.
По одной кривой отношение масс звезд не определишь.
Приходится довольствоваться тем, что есть.
Что же можно узнать, имея в руках одну кривую лучевой
скорости? Давайте вначале решим простенькую систему четырех уравнений.
Предположим, что орбиты
звезд двойной круговые. Очевидно, сумма радиусов орбит звезд равна большой
полуоси двойной системы. Это
первое уравнение:
г1 + г2 = a .
В качестве второго уравнения возьмем условие,
определяющее расстояние от центра масс двойной до каждой
из звезд:
M1r1 =
M2r2
Третий закон Кеплера (2) будет третьим нашим уравнением:
a3/P2 = G/4 pi2 (M1 +
M2)
Построив
кривую лучевых скоростей звезды 1, мы можем определить размах
синусоиды
(амплитуду). Разделим его пополам и обозначим К1 Эта величина
называется полуамплитудой. Каков ее физический смысл? Так
как, согласно эффекту Доплера, сдвиг длины волны пропорционален проекции
скорости движения звезды на луч
зрения (лучевой скорости), то ясно, что К1
проекция
орбитальной скорости звезды 1 на луч зрения. При круговом равномерном
движении орбитальная скорость равна длине окружности, деленной на период.
Значит,
К1 = (2 pi a/P) sin i
Это и есть
наше четвертое уравнение. Подставляя последовательно одно уравнение в другое,
избавляясь от г1, г2 и a
получим одно уравнение, содержащее пять величин:
массы звезд, угол наклона двойной системы, период ее
обращения и полуамплитуду кривой лучевых скоростей.
Причешем это уравнение так, чтобы в правой его части остались известные
или измеряемые прямо величины. Все остальное пусть остается в левой части.
Эту
левую часть называют функцией масс. Вот как она выглядит:
f1(M) = M23 sin3 i
/(M1 +M2)2 = P K3/ (2 pi G)
(6)
Точнее,
f1(M) - это
функция масс, определенная по линиям первой звезды. Из соображений симметрии
ясно,
что если заменить индекс 1 на индекс 2, мы получили бы
такую же комбинацию, только М2 нужно заменить на
М1. Это была
бы функция масс, определенная по спектральным линиям звезды 2.
Но вернемся к
формуле (6).
Обратите внимание, функция масс имеет размерность
массы. Обычно ее измеряют в массах Солнца. Чтобы почувствовать физику ,
давайте проанализируем зависимость функции масс от полуамплитуды кривой
лучевых
скоростей. Пусть период двойной не меняется. Будем
мысленно увеличивать полуамплитуду К1 Что это значит? Звезда
1
движется все быстрее и быстрее. Но движется-то она в гравитационном поле
звезды 2. Значит,
должна расти ее масса. Поэтому в формуле (6) в числителе стоит куб массы
второй звезды. На самом деле, конечно, полуамплитуда К1 есть величина
постоянная. Наш
мысленный эксперимент моделирует перебор разных
двойных с одним орбитальным периодом и углом наклона. Этот эксперимент
показывает, что функция масс содержит в себе информацию (правда, в скрытом
виде)о массе звезды 2.
Заметьте, что функция масс определяется спектроскопически.
Зная функцию масс, конечно, не найдешь массы
звезд по отдельности и угол наклона i. Нужна дополнительная
информация, получаемая, например, из кривой
блеска. Почему же мы уделили ей так много внимания?
Функция масс обладает очень важным свойством.
Разделим f1(M) на массу второй звезды:
f1(M)/ M2 = (M2/(M2 +
M2))3 sin3 i
Легко
убедиться, что правая часть последнего равенства
меньше или равна единице. Значит, справедливо неравенство
M2 > = f1(M)
Это
неравенство имеет большую практическую ценность.
Представьте себе такую ситуацию. Вы астроном. В одну
прекрасную ночь вам удалось снять спектр весьма загадочной звезды.
Собственно, сначала в ней не было ничего загадочного. Вы отсняли спектр,
проявили фотопластинку (после того, как выспались) и внимательно ее
рассмотрели. На пластинке оказался обычный спектр
одиночной звезды. Но вы так просто не сдаетесь и на
следующую ночь, благо она тоже оказалась прекрасной,
снимаете спектр звезды еще раз. Повторяете все снова.
Теперь у вас два спектра одной и той же звезды. Вы начинаете их сравнивать и
вдруг замечаете: все линии второго спектра сдвинулись по отношению к линиям
спектра, полученного в первую ночь. Дело ясное: вы открыли
двойную звезду. Ни в одном каталоге эта звезда не значится как двойная. А
каждый астроном, прежде чем наблюдать какую-то звезду, просматривает
каталоги
и статьи: нет ли чего о ней?!
Итак, звезда двойная. Однако возникает вопрос: почему в
спектре не видны линии второй звезды? Ответ
для вас ясен: вторая звезда слабее и спектр ее не заметен
на фоне первой звезды. Но от этого вторая звезда становится еще загадочнее.
Вам хочется что-нибудь узнать
о невидимке. Вы тратите еще месяц, и у вас в руках кривая блеска чистая
синусоида с периодом 1,2 дня. Полуамплитуда оказалась равной К1 =400
км/с. Подставив
эти значения в формулу (6), нашли функцию масс
/i (М) = 8М (солнечных). Теперь вы знаете, что каким бы ни был наклон двойной, какова
бы ни была масса видимой звезды
M1, масса
невидимки заведомо больше 8 масс Солнца.
Иногда такая информация оказывается крайне важной.
Далее мы убедимся в этом.
Продолжение следует
Обозрение "Физические явления на небесах" профессора В.М.Липунова.
�